Effectiveness of potential antiviral treatments in COVID-19 transmission control: a modelling study

Abstract

Background

Novel coronavirus disease 2019 (COVID-19) causes an immense disease burden. Although public health countermeasures effectively controlled the epidemic in China, non-pharmaceutical interventions can neither be maintained indefinitely nor conveniently implemented globally. Vaccination is mainly used to prevent COVID-19, and most current antiviral treatment evaluations focus on clinical efficacy. Therefore, we conducted population-based simulations to assess antiviral treatment effectiveness among different age groups based on its clinical efficacy.

Methods

We collected COVID-19 data of Wuhan City from published literature and established a database (from 2 December 2019 to 16 March 2020). We developed an age-specific model to evaluate the effectiveness of antiviral treatment in patients with COVID-19. Efficacy was divided into three types: (1) viral activity reduction, reflected as transmission rate decrease [reduction was set as v (0–0.8) to simulate hypothetical antiviral treatments]; (2) reduction in the duration time from symptom onset to patient recovery/removal, reflected as a 1/γ decrease (reduction was set as 1–3 days to simulate hypothetical or real-life antiviral treatments, and the time of asymptomatic was reduced by the same proportion); (3) fatality rate reduction in severely ill patients (f_c) [reduction (z) was set as 0.3 to simulate real-life antiviral treatments]. The population was divided into four age groups (groups 1, 2, 3 and 4), which included those aged ≤ 14; 15–44; 45–64; and ≥ 65 years, respectively. Evaluation indices were based on outbreak duration, cumulative number of cases, total attack rate (TAR), peak date, number of peak cases, and case fatality rate (f).

Results

Comparing the simulation results of combination and single medication therapy s, all four age groups showed better results with combination medication. When 1/γ = 2 and v = 0.4, age group 2 had the highest TAR reduction rate (98.48%, 56.01–0.85%). When 1/γ = 2, z = 0.3, and v = 0.1, age group 1 had the highest reduction rate of f (83.08%, 0.71–0.12%).

Conclusions

Antiviral treatments are more effective in COVID-19 transmission control than in mortality reduction. Overall, antiviral treatments were more effective in younger age groups, while older age groups showed higher COVID-19 prevalence and mortality. Therefore, physicians should pay more attention to prevention of viral spread and patients deaths when providing antiviral treatments to patients of older age groups.

Background

On January 30, 2020, the World Health Organization (WHO) declared novel coronavirus disease 2019 (COVID-19) a public health emergency of international concern [1] and a challenging public health crisis [2]. Many studies have reported that COVID-19 has caused an enormous disease burden globally [3, 4], and it continues to spread vigorously in the United States, Brazil, and other countries [5]. Presently, international epidemic prevention and control strategies for COVID-19 include pharmaceutical interventions (PIs) (antiviral treatment and vaccination) and non-pharmaceutical interventions (NPIs) [isolation, wearing of masks, social distancing (closing of schools, cancellation of collective activities, and crowd gathering restrictions), and tourism restrictions]. The effectiveness of NPIs have been proven in many countries [6,7,8,9,10,11,12,13]. China, especially, successfully controlled the first wave of the COVID-19 outbreak by strictly implementing various public health policies, including the timely isolation of cases, contact tracing, social distancing control, and entertainment activity restriction [12, 14,15,16]. Furthermore, Republic of Korea's timely public health measures also achieved remarkable results in epidemic control [17].

NPIs implemented were dependent on a variety of factors, such as social and economic systems and required good cooperation from the public. Further, ‘lockdowns’ produced substantial economic hardship [18]. Meanwhile, model analysis showed that characteristics of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) allow it to stably coexist with people [19]. When SARS-CoV-2 reaches the endemic phase, its overall pathogenicity in the population may be equivalent to that of common cold viruses [19]. NPIs can neither be maintained indefinitely nor conveniently implemented in all countries. Furthermore, evidence has already indicated that these types of public health measures alone may be insufficient for controlling COVID-19 [20].

As work gradually resumes, and productivity increases, various provinces and cities in China are facing the potential risk of an additional wave of COVID-19 outbreak [21]. Since the virus continues to spread, PIs will be essential for preventing and controlling the spread of COVID-19 [14, 22], thereby reducing social control dependence [23]. Recently, numerous studies have been published on the developmental process, safety, and efficacy of COVID-19 vaccines [24,25,26,27,28,29,30]. Moreover, our team has conducted relevant research on this subject [31]. However, the primary role of vaccination is to prevent COVID-19.

Approximately 2000 ongoing trials on the efficacy of pharmacological therapy against SARS-CoV-2 infection have been registered in the WHO International Clinical Trials Registry Platform. Nevertheless, no specific drug has been confirmed to be effective [32]. A systematic review and network meta-analysis of the efficacy and safety of 31 existing drugs revealed that anti-inflammatory agents (tocilizumab, anakinra, and gamma globulin) and remdesivir might improve the prognosis of patients with COVID-19. Furthermore, hydroxychloroquine may be associated with cardiac and non-cardiac safety risks after clearing the virus [33], and dexamethasone reduces the 28-day mortality risk in severely ill patients, especially in those receiving invasive ventilation [34]. The efficacy of antiviral treatments requires further verification, and most recent studies evaluating antiviral treatments focus on clinical efficacy specifically. Further, many studies have shown that the prevalence and case fatality rate of COVID-19 varies among different age groups [15, 35,36,37,38]. Therefore, we aimed to evaluate the effectiveness of COVID-19 antiviral treatments among different age groups based on the hypothetical or real-life efficacy of antiviral treatments from the public health perspective. On the one hand, we hope to predict the public health effects of existing antiviral treatments; on the other hand, we hope to provide a model that can be directly applied to evaluate the effectiveness of novel antiviral treatments based on their clinical efficacy, when such antiviral treatments becomes available in the future.

Methods

Data source and study design

The following previously published data were collected from patients with COVID-19 in Wuhan from 2 December 2019 to 16 March 2020: age, clinical severity classification (mild, moderate, severe, and critical), date of onset, and date of death [31]. The study population was divided into four age groups based on previous study findings [31, 36, 39], as follows: group 1, ≤ 14 years; group 2, 15–44 years; group 3, 45–64 years; and group 4, ≥ 65 years. The total population in Wuhan City at the time of the prior study was 11 080 996 for those aged ≤ 14, 15–44, 45–64, and ≥ 65 years, the number of individuals in Wuhan city was 1 256 552; 5 210 885; 3 374 388; and 1 239 171, respectively [31].

Age-specific model

An age-specific Susceptible–exposed–symptomatic–asymptomatic-recovered/removed (SEIAR) model was developed previously [31, 39]. To implement the model, individuals were divided into the following five categories: susceptible (S), exposed (E), symptomatic (I), asymptomatic (A), and recovered/removed (R). The rate of infection transmissibility for each age group was estimated using the model, and the process of data fitting detailed previously [31] depended on the following assumptions:

• 1) S individuals in age group i (the range of i and j was 1–4, indicating different age groups) were infected by exposure to I and A individuals in age group i and other age groups. The transmission rates of S were β and κβ (0 < κ < 1) after effective contacts with I and A, respectively.

• 2) The transmission rate (β) was divided into two categories: β_ii (within the age group i) and β_ij (age groups i to j).

• 3) Parameter p was set as the proportion of A individuals, whereas incubation and latent periods of I and A were 1/ω and 1/ω′, respectively.

• 4) The times from categories I and A to category R were set as 1/γ and 1/γ′, respectively.

• 5) The case fatality rate was set as f for members of category I who died after infection.

The flowchart of this model is presented in our previously published paper, as well as some parameter estimations, such as k, p, ω, ω′, γ, and γ′ [31]. The equations used in the current model are as follows:

$$i\ne j$$

$$\frac{d{S}_{i}}{dt}=-{\beta }_{ii}{S}_{i}\left({I}_{i}+\kappa {A}_{i}\right)-{\beta }_{ji}{S}_{i}\left({I}_{j}+\kappa {A}_{j}\right)$$

$$\frac{d{E}_{i}}{dt}={\beta }_{ii}{S}_{i}\left({I}_{i}+\kappa {A}_{i}\right)+{\beta }_{ji}{S}_{i}\left({I}_{j}+\kappa {A}_{j}\right)-\left(1-p\right)\omega {E}_{i}-p{\omega }^{^{\prime}}{E}_{i}$$

$$\frac{d{I}_{i}}{dt}=\left(1-p\right)\omega {E}_{i}-\gamma {I}_{i}-{f}_{i}{I}_{i}$$

$$\frac{d{A}_{i}}{dt}=p{\omega }^{^{\prime}}{E}_{i}-{\gamma }^{^{\prime}}{A}_{i}$$

$$\frac{d{R}_{i}}{dt}={\gamma I}_{i}+{{\gamma }^{^{\prime}}A}_{i}$$

$$\frac{d{S}_{j}}{dt}=-{\beta }_{jj}{S}_{j}\left({I}_{j}+\kappa {A}_{j}\right)-{\beta }_{ji}{S}_{j}\left({I}_{i}+\kappa {A}_{i}\right)$$

$$\frac{d{E}_{j}}{dt}={\beta }_{jj}{S}_{j}\left({I}_{j}+\kappa {A}_{j}\right)+{\beta }_{ji}{S}_{j}\left({I}_{i}+\kappa {A}_{i}\right)-\left(1-p\right)\omega {E}_{j}-p{\omega }^{^{\prime}}{E}_{j}$$

$$\frac{d{I}_{j}}{dt}=\left(1-p\right)\omega {E}_{j}-\gamma {I}_{j}-{f}_{j}{I}_{j}$$

$$\frac{d{A}_{j}}{dt}=p{\omega }^{^{\prime}}{E}_{j}-{\gamma }^{^{\prime}}{A}_{j}$$

$$\frac{d{R}_{j}}{dt}={\gamma I}_{j}+{{\gamma }^{^{\prime}}A}_{j}$$

$$N={S}_{i}+{E}_{i}+{I}_{i}+{A}_{i}+{R}_{i}$$

With subscripts i and j (i ≠ j) representing age groups 1–4.

Based on the existing data stage grouping, we performed data fitting and calculated the dissemination capacity of the four age groups (stages 1, 2, 3, and 4 occurred from 2 December 2019 to 23 January 2020; 24 January to 2 February 2020; 3 February to 18 February 2020; and 19 February 2020 to 16 March 2020, respectively; the details of which are shown in our previous article [31]). The results of data fitting are shown in Additional file 1: Fig. S1 and Additional file 3: Table S1.

Age-specific model for antiviral treatments

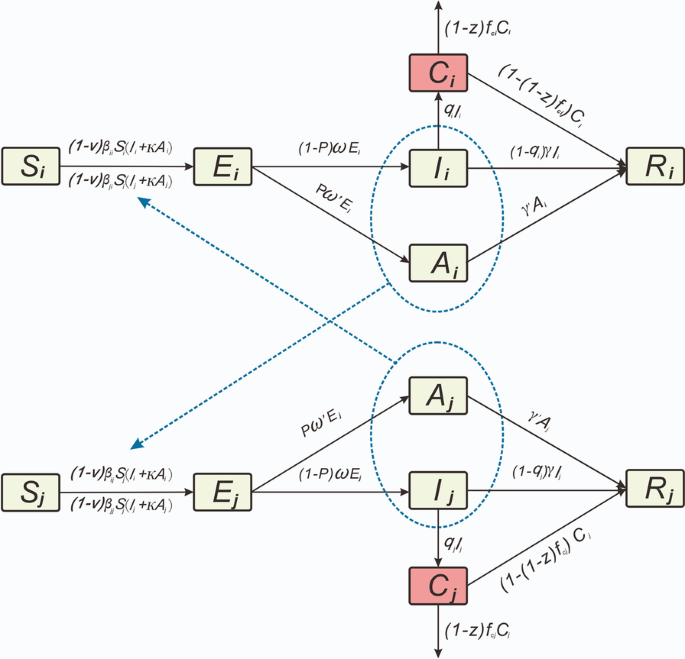
Firstly, death only occurred in severely ill patients [15], therefore, we classified all patients as either severely (severe and critical) or non-severely ill (mild and moderate), according to the COVID-19 clinical severity classification of each patient. Based on the existing age-specific model [39, 40], we distinguished severely ill patients from category I patients. The framework of the SEIAR model for antiviral treatment is shown in Fig. 1. In this model, the population was divided into six categories, as follows: susceptible (S), exposed (E), symptomatic (I), severely ill patients (C), asymptomatic (A), and recovered/removed (R). When implementing the model, the following assumptions were made:

• 1) S individuals in age group i (the range of i and j was 1–4, indicating different age groups) were infected by exposure to I and A individuals in age group i and other age groups. The transmission rates of S were β and κβ (0 < κ < 1) after effective contacts with I and A, respectively.

• 2) The transmission rate (β) was divided into two categories, as follows: β_ii (within the age group i) and β_ij (age group i to j), and the reduction ratio of β was set as v (the initial value of v was 0).

• 3) Parameter p was set as the proportion of A individuals, whereas the incubation and latent periods of I and A were 1/ω and 1/ω′, respectively.

• 4) The ratio of severely ill patients in age group i was set as q_i, and the fatality rate of severely ill patients in age group i was set as f_ci. The reduction ratio of f_ci was set as z (initial value of z was 0), and the number of people who changed from C_i to R_i was (1 − [1 − z] f_ci) C_i at time t.

• 5) Durations needed to change from categories I and A to category R were set as 1/γ and 1/γ′, respectively. Therefore, the numbers of people who transitioned from I to R and A to R, respectively, were γI and γ′A at time t.

Fig. 1

The framework of Susceptible–Exposed–Symptomatic–Asymptomatic-Recovered/Removed (SEIAR) model

The following equations were used in the model:

$$i\ne j$$

$$\frac{d{S}_{i}}{dt}=-(1-\mathrm{v}){\beta }_{ii}{S}_{i}\left({I}_{i}+\kappa {A}_{i}\right)-(1-\mathrm{v}){\beta }_{ji}{S}_{i}\left({I}_{j}+\kappa {A}_{j}\right)$$

$$\frac{{dE_{i} }}{dt} = \left( {1 - v} \right)\beta_{ii} S_{i} \left( {I_{i} + \kappa A_{i} } \right) + \left( {1 - v} \right)\beta_{ji} S_{i} \left( {I_{j} + \kappa A_{j} } \right) - \left( {1 - p} \right)\omega E_{i} - p\omega^{\prime}E_{i}$$

$$\frac{{dA_{i} }}{dt} = p\omega^{\prime}E_{i} - \gamma^{\prime}A_{i}$$

$$\frac{d{I}_{i}}{dt}=(1-p)\omega {E}_{i}-{q}_{i}{I}_{i}-(1-{q}_{i})\gamma {I}_{i}$$

$$\frac{d{C}_{i}}{dt}={q}_{i}{I}_{i}-(1-z){f}_{ci}{C}_{i}-(1-\left(1-\mathrm{z}\right){f}_{ci}){C}_{i}$$

$$\frac{d{R}_{i}}{dt}=\left(1-\left(1-\mathrm{z}\right){f}_{ci}\right){C}_{i}+\left(1-{q}_{i}\right)\gamma {I}_{i}+{\gamma }^{^{\prime}}{A}_{i}$$

$${X}_{i}=(1-p)\omega {E}_{i}$$

$$\frac{d{S}_{j}}{dt}=-(1-\mathrm{v}){\beta }_{jj}{S}_{j}\left({I}_{j}+\kappa {A}_{j}\right)-(1-\mathrm{v}){\beta }_{ij}{S}_{j}\left({I}_{i}+\kappa {A}_{i}\right)$$

$$\frac{{dE_{j} }}{dt} = \left( {1 - v} \right)\beta_{jj} S_{j} \left( {I_{j} + \kappa A_{j} } \right) + \left( {1 - v} \right)\beta_{ij} S_{j} \left( {I_{i} + \kappa A_{i} } \right) - \left( {1 - p} \right)\omega E_{j} - p\omega^{\prime}E_{j}$$

$$\frac{{dA_{j} }}{dt} = p\omega^{\prime}E_{j} - \gamma^{\prime}A_{j}$$

$$\frac{d{I}_{j}}{dt}=(1-p)\omega {E}_{j}-{q}_{j}{I}_{j}-(1-{q}_{j})\gamma {I}_{j}$$

$$\frac{d{C}_{j}}{dt}={q}_{j}{I}_{j}-(1-z){f}_{cj}{C}_{j}-(1-\left(1-\mathrm{z}\right){f}_{cj}){C}_{j}$$

$$\frac{d{R}_{j}}{dt}=\left(1-\left(1-\mathrm{z}\right){f}_{cj}\right){C}_{j}+\left(1-{q}_{j}\right)\gamma {I}_{j}+{\gamma }^{^{\prime}}{A}_{j}$$

$${X}_{j}=(1-p)\omega {E}_{j}$$

$$N={S}_{i}+{E}_{i}+{I}_{i}+{A}_{i}+{R}_{i}+{S}_{j}+{E}_{j}+{I}_{j}+{A}_{j}+{R}_{j}$$

Parameter estimation

Parameter values used in the model and the methods used for their determination are detailed in Table 1. The model had 30 parameters (β_ii, β_ij, β_jj, β_ji, f_ci, q_i, κ, p, ω, ω′, γ and γ′).

• 1) We used an age-specific model to fit data, and obtained results of four stages. The parameters of β that we used for the simulation were the results determined during stage 1 (Additional file 2: Fig. S2).

• 2) Based on the analysis of data, ratios of severely ill patients (q_i) were 3.25%, 10.99%, 19.14%, and 37.79% for age groups 1, 2, 3, and 4, respectively. Fatality rates for severely ill patients (f_c) of the groups were 5.00%, 5.16%, 18.20%, and 39.79%, respectively.

• 3) A previous study indicated that 4.11% and 6.30% of individuals would become infected after close contact with A and I patients, respectively [41]. Moreover, in the study, k was set as 0.65 [31]; therefore, in this study, we assumed that the transmissibility of A infections was 0.65 times that of I infections. Further, it has been reported that the transmissibility of I is 3.9 times that of A, and an asymptomatic individual may infect 11 people [42]. Another study set κ as 1.0 [39]. Based on previous results, we set the range of k to 0–1.

• 4) Values of p used in different studies have varied. For instance, the proportion of A patients in the Diamond Princess cruise ship was 17.9% [95% confidence interval (CI): 15.5–20.2%] [43] and 20.75% in Ningbo City [41]. In addition, a study estimated an A ratio of 30.8% (95% CI: 7.7–53.8%) using a binomial distribution [44], whereas another study reported that A patients constituted 5% to 28% of all patients with COVID-19 [35]. Furthermore, it was also reported that the A ratio could reach 78% [45]. Therefore, since we set the A proportion (p) to 0.36 previously (1.6–78%) [31], we used the same value in the present study (Fig. 2-a).

• 5) A previous study revealed that the incubation period early in the epidemics in Wuhan City was 4 days (interquartile range: 2–7 days) [46], whereas other studies indicated that the incubation period in Wuhan [47] and Ningbo [41] raged from 2–14 days and 2–18 days, respectively. In addition, another study reported an incubation period of 5.1 days (95% CI: 4.5–5.8) [48]. Therefore, we set the incubation period to 5 days previously (ω = ω’ = 0.2) based on the median incubation periods of multiple studies [31]. The same value was used in the present study. We show incubation periods reported in many different studies in Fig. 2c, and, based on current findings, determined that setting the incubation period as 5 days is representative of published data.

• 6) Various studies have reported the following durations from symptom onset to hospitalisation: 6.39 (range: 1.00–8.83), 7, 4–6, and 4.1–7.5 days [36, 49,50,51]. Moreover, right-truncated data indicated that the time from illness onset to hospitalisation ranged from 2.7 to 8.0 days [47]. Therefore, in our previous study, the infectious periods for I patients were set to 5 days (γ = 0.2) [31]. The same value, which was based on the median infectious period determined in multiple studies, was used in the present study. We show infectious periods of I determined previously in Fig. 2-b. A prior study indicated that the median infectious period of 24 A patients was 9.5 days (range: 1–21 days) [52]. Therefore, we set γ’ as 0.1 in the model [31].

Table 1 Description and values of parameters in the age-specific SEICAR model

Fig. 2

Summary of reported parameters of p, ω, γ. a Reference about proportion of asymptomatic. b Reference about infectious period of asymptomatic. c Reference about incubation/latent period

Antiviral treatment simulation

Existing antiviral treatments and their clinical efficacies are shown in Table 2. Based on current research, we divided the effectiveness of antiviral treatment into three types: (1) reducing transmission (β); (2) decreasing the infectiousness of I and A (1/γ and 1/γ’); and (3) reducing the fatality rate of severely ill patients (f_c).

• 1) A prior study showed that remdesivir efficiently inhibited viral infection in a human cell line (human liver cancer Huh-7 cells) sensitive to SARS-CoV-2; thus, remdesivir can reduce the infectivity of COVID-19 to an extent [46]. Similarly, researchers determined that chloroquine has antiviral activity and can synergistically enhance antiviral effects of remdesivir in vivo [46]. In the model, antiviral treatments capable of reducing viral activity were revealed by decreases in β. However, existing studies have not specified the extent to which antiviral treatments reduce β values, and therefore, the reduction of β was determined by adjusting the value of v (0–0.8) to simulate that of hypothetical antiviral treatments.

• 2) Previous studies have shown that remdesivir might not improve recovery or reduce mortality in patients with COVID-19 [53, 54]. However, a preliminary study in the United States, involving many hospitals globally, demonstrated that using remdesivir in hospitalised patients with COVID-19 receiving oxygen therapy shortened their recovery time from 15 to 11 days and reduced risk of respiratory infections [55]. Some clinical trials have shown that the recovery time of patients with COVID-19 who use remdesivir is 31% faster than that of patients provided a placebo [56]. For severely ill patients, combined use of ribavirin with interferon beta-1b and lopinavir/ritonavir safely and efficiently shortens the duration and reduce symptoms of viral infection in patients with mild-to-moderate disease, with mild side effects [57]. In addition, other studies have shown that chloroquine phosphate can shorten the clinical course of COVID-19 [36]. In this model, antiviral treatments capable of reducing the duration needed to transition from categories I and A to category R were reflected in 1/γ and 1/γ′ decrease. The reduced duration needed to transition from category I was set to 1–3 days to simulate hypothetical or real-life antiviral treatments, and the duration from category A was reduced proportionally to 1/γ.

• 3) Dexamethasone use reduced the number of deaths among patients with COVID-19 using ventilators by 30% [34, 58]. In addition, the improvement effect of tocilizumab on severely or critical ill patients with COVID-19 has also been confirmed. Futher, interferon-alpha 2b was reported to affect survival in patients with COVID-19 [59,60,61]. Another research team successfully identified multiple highly active neutralising antibodies in the plasma of recovered patients [62]. Experimental treatments using plasma of recovered patients have also been shown to significantly effective in severely and critically ill patients [63], but their widespread use is not feasible at present. In the model, antiviral treatments capable of reducing fatality rates of severely ill patients were reflected as decreases in f_c (reduction was set as z). We set z as 0.3, to simulate real-life antiviral treatment.

Table 2 Summary of existing antiviral treatments

Evaluation index

The evaluation indices were as follows:

• 1) Outbreak duration (OD, days): the number of days from the infection of the first patient to the recovery or death of the last patient.

• 2) Cumulative number of cases (CNC): the number of COVID-19 patients during the outbreak.

• 3) Total attack rate (TAR): the ratio of the cumulative number of cases to the total population.

• 4) Peak date (PD): the date on which the maximum number of cases was observed.

• 5) Number of peak cases (NPC): the number of cases recorded on the peak date.

• 6) Case fatality rate (f): the ratio of the number of deaths to the cumulative number of cases identified during the outbreak.

The values of these indices were the simulated number of cases provided different antiviral treatments rather than the actual number.

Simulation methods and statistical analysis

Berkeley Madonna 8.3.18 (developed by Robert Macey and George Oster, University of California at Berkeley; copyright ©1993–2001 Robert I. Macey & George F. Oster) was employed for curve fitting and simulation. We used the same simulation methods (Runge–Kutta fourth-order method with the tolerance set to 0.001) as described previously [64,65,66,67,68,69]. Berkeley Madonna was used to adopt the curve fitting of the least root-mean-square deviation. Goodness of fit was judged by the coefficient of determination (R²) value, which was calculated using IBM SPSS Statistics for Windows, version 21.0 (IBM Corp. Armonk, NY, USA) and Microsoft Office Excel 2016 (Microsoft, Redmond, WA, USA).

Sensitivity analysis

In this study, two parameters were used to analyse the sensitivity of the model: k (0–1) and p (0.016–0.78), each was split into 1000 values according to its range. The mean and standard deviation (SD) were calculated for sensitivity analysis.

Results

Results of the antiviral treatment simulation

This study evaluated the intervention effect of COVID-19 therapies by simulating several antiviral treatments with different efficacies. Overall, we observed age-dependent differences.

Age group-specific results obtained without intervention indicated that an increase in age was associated with increased TAR and f, as well as advanced PD. However, with an increase in age, CNC, NPC, and OD initially increased and then decreased. Changes in β, γ andγ’ did not vary. When β, γ, andγ’ of each age group remained unchanged, changes in f_c did not affect the trend and severity of the epidemic, but reduced f. However, by reducing β without changing f_c, γ, and γ’, we observed that CNC, NPC, and TAR continued to decrease, while OD was prolonged, and PD continued to be delayed. Although f continued to fall, β needed to be reduced by 70% in age group 1 and 80% in age groups 2, 3, and 4 to completely control the epidemic. When β and f_c remained unchanged, γ and γ’ increased, and CNC, NPC, and TAR continued to decrease; nevertheless, OD was prolonged, and PD continued to be delayed (Additional file 4: Table S2, Additional file 5: Table S3, Additional file 6: Table S4, Additional file 7: Table S5).

When different antiviral treatments were used, the TAR reduction rate was higher than f for all age groups, and the reduction of different age groups varied. When comparing the reduction of TAR with f when only one type of antiviral treatment was used, we found that changes in β and γ had the greatest effects on TAR and f, respectively. When the value of v was 0.7, age group 2 had the highest TAR reduction rate (95.78%). However, when the value of 1/γ was 2, age group 1 had the highest f reduction rate (64.56%).

Comparing the simulation results of combination and single medications, all four age groups showed better results with the combination medication. When 1/γ = 2, and v = 0.6 or 1/γ = 2, v = 0.6, and z = 0.3, age group 1 had the highest TAR reduction rate. However, When 1/γ = 2 and v = 0.4 or 1/γ = 2, v = 0.4, and z = 0.3, age group 2–4 had the highest TAR reduction rates. The TAR reduction rate of age group 2 was the highest among the 4 age groups considered (98.48%, from 56.01 to 0.85%) (Fig. 3b), whereas the absolute TAR reduction value of age group 3 was highest among the 4 age groups (0.6070, from 0.6292 to 0.0222) (Fig. 3c). When 1/γ = 2, z = 0.3, and v = 0.1, age group 1 had the highest f reduction rate. However, when v = 0.4, z = 0.3, and 1/γ = 2, age group 2–4 had the highest f reduction rate. The f reduction rate of age group 1 was the highest among all 4 age groups (83.08%, from 0.71 to 0.12%) (Fig. 4a). whereas the absolute f reduction value of age group 4 was the highest (0.1451, from 0.2938 to 0.1487) (Fig. 4d). Details are shown in Additional file 8: Table S6, Additional file 9: Table S7, Additional file 10: Table S8, Additional file 11: Table S9.

Fig. 3

Evaluation of the effectiveness of potential antiviral treatments (with highest TAR reduction in each age group). a ≤ 14 years; b15–44 years; c 45–64 years; d ≥ 65 years

Fig. 4

Evaluation of the effectiveness of potential antiviral treatments (with highest f reduction in each age group). a ≤ 14 years; b 15–44 years; c 45–64 years; d ≥ 65 years

The results of the sensitivity analysis

In this study, we found that parameters k and p used in the model were included in the range of simulated mean ± SD values (Fig. 5). These two parameters were not sensitive to the model.

Fig. 5

The results of sensitivity analysis. a κ = 0.65, ≤ 14 years; b: κ = 0.65, 15–44 years; c κ = 0.65, 45–64 years; d κ = 0.65, ≥ 65 years; e p = 0.36, ≤ 14 years; f p = 0.36, 15–44 years; g p = 0.36, 45–64 years; h p = 0.36, ≥ 65 years

Discussion

This study was based on our existing age-specific transmissibility model of SARS-CoV-2, which is the first model to quantify the transmissibility of COVID-19 within and between different age groups [39]. We pursued an innovative approach by incorporating multiple factors, such as the ratio of severely ill patients (q) and the fatality rate of severely ill patients (f_c) of each age group, to build an antiviral treatments evaluation model for a set of age groups. The model was used to assess intervention efficacy of different antiviral treatments by changing parameters as needed. However, most current COVID-19 pharmacological therapies remain at the clinical efficacy evaluation stage, and the reliability of antiviral treatments require further exploration. The focus of this study was to evaluate the effectiveness of antiviral treatments in different age groups from a public health perspective, using hypothetical or real-life antiviral treatments.

Parameters of this study were as follows: β and disease natural history parameters. β parameters were obtained from the results of curve fitting. The date separating stages 1 and 2 was 23 January 2020, as Wuhan declared a lockdown on 22 January 2020. Thus, we can approximately regard the first stage as the non-intervention stage. It is universally accepted that β parameters of stage 1 represent the transmissibility of the disease in its natural state [31]. This is also the possible reason why the number of simulated cases exceeded the actual number of cases in Wuhan. Under this premise, we excluded the efficacy of other possible interventions when evaluating the efficacy of antiviral treatments. Moreover, results of R² calculations showed that the model fitted well.

There are two sources of disease natural history parameters: the ratio of severely ill patients (q) and the fatality rate of severely ill patients (f_c), which were calculated using real data. Remaining parameters (κ, p, ω, ω′, γ, and γ′) were quoted from prior studies. Sensitivity analyses were performed for parameters of k and p, and other values were based on published findings. Median values of published findings were calculated.

Some studies have reported variations in COVID-19 prevalence between different age groups [35, 36, 39], akin to our study findings. Without intervention, groups 1 and 4 had the lowest and highest TAR values, respectively; these were similar to findings of a study conducted in Hungary [37]. Another three-age-group study using a generalised linear mixed model revealed that people aged ≥ 65 years had a higher risk of becoming infected with SARS-CoV-2 than those aged 15–64 years [70]. It was speculated that reasons for these age-based differences may be due to increased rates of underlying diseases observed in adults aged 65 years [38] that predisposed them to COVID-19 infection due to their low level of immunity. Differing fatality rates observed in severely ill patients did not have an impact on the epidemic. This may be due to the fact that most severely ill patients are in the intensive care units and reducing the fatality rate will not affect other populations.

When antiviral treatments reduce β or γ and γ’, each age group had a different degree of control. This may have been due to differences in disease transmissibility observed for each age group. For example, the age group 2 population was the largest group, which may suggest that the decrease in β had the greatest impact on the TAR in the age group. Moreover, we hypothesised that different age groups had different sensitivities to different antiviral treatments. However, the specific antiviral treatment sensitivity of each age group requires further pharmacological exploration. Furthermore, differences in autoimmunity may have an effect on the effectiveness of potential antiviral treatments.

Some parameters were not included in the study, such as data associated with non-severe cases and that of immunity acquisition over time. Future scenario predictions may be inaccurate and unpredictable, and current calculation methods may overestimate or underestimate the effectiveness of potential antiviral treatments throughout the population considered.

Conclusions

Antiviral treatments are more effective for COVID-19 transmission control than for mortality reduction. Overall, antiviral treatments were most effective when used to treat younger age groups, while older age groups showed higher disease prevalence and mortality. Therefore, older age groups require more attention with respect to the use of antiviral treatments in clinical practice.